IDC402 Non Linear Dynamics
Tuesday, February 1, 2022
Universality of Figenbaum
$x_{n+1} = \sin(x_n)$
Superstable orbit ratio
$R_i$ is a superstable fixed point of a period $2^{i}$ orbit.
Let $\delta_m$ be the distance between $y=1/2$ and nearest other $2^m-1$ points in the cycle - which happens to be point where one half period displaced from the critical point
$\delta = F^{2^{m-1}}$
$\frac{\delta_m}{\delta_{m+1}} \to -2.50280 \equiv\alpha$
What happens beyond $r_\infty$?
- Chaotic bands -
- Windows of odd periods - third kind of [2022-01-18#Bifurcations|bifurcation]
Tangent Bifurcation
No solutions $\to$ 2 new solutions, 1 stable, 1 unstable.
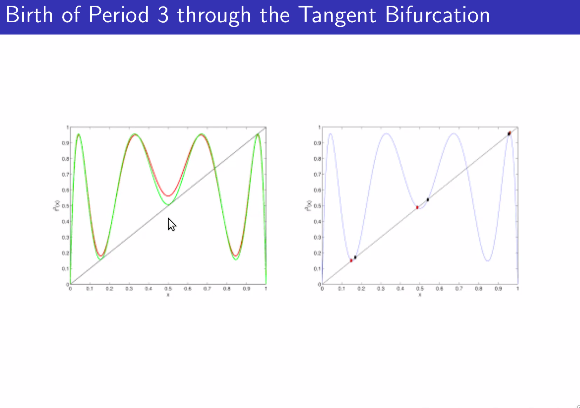
Tangent points form new solutions, which may give 1 stable and 1 unstable points. If the number of tangents is odd, then we have an odd number of points
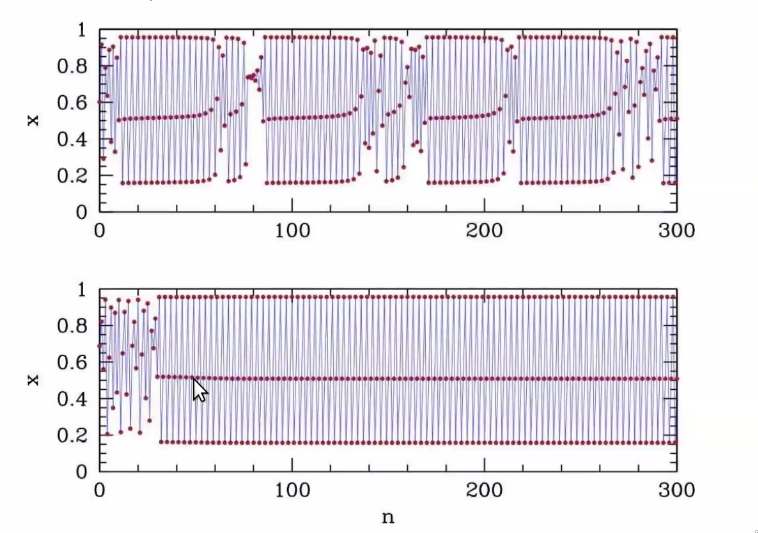
Intermittency
Where close to the period 3 cycles, the time series has laminar(almost 3 cycle) sections interrupted by turbulent flows. The closer we get to actual 3 cycle, the longer the laminar sections get larger and larger.