Term Paper 2

This work is a submission for the course Modelling Complex Systems(IDC-631) for the year 2020-21 Spring (Even) Semester by Dhruva Sambrani, MS18163

4.7 μs

Abstract

This paper laregly recreates the paper[soc] by Bak, Per and Tang, Chao and Wiesenfeld, Kurt on models that exhibit self-organized criticality. These models show certain structures repetitive structures and show distinctive power laws in certain properties.

The specific model I have looked at is the Sandpile model, which has a relaxation time frequency having a log-log slope of between 1 to 2. This paper first introduces some working definitions and their equivalent definition in Julia[julia] code.

First a pretty, but small simulation is shown which also verifies that the model is infact correctly translated. Post this, more rigourous analysis is done, and finally results and observations are mentioned

15.8 μs

How to read the paper

This paper is made using the Pluto[pluto] Package which provides an interface which can show both code and theory side by side, which will hopefully enhance the understanding of the work and also provide a reproducable implementation without having to go into the details of it. Those who wish to read the paper for the theory and results can easily skip over the code and still understand everything. Those who are attempting to recreate the work can use the code as a guide. However, in the interest of keeping the code aligned to the topic at hand, certain auxillary functions have been hidden. The content of these hidden cells can be found in the executable version of this notebook here

1.1 ms

94.8 μs

Code Setup

5.5 μs

Packages used

The Plots.jl[plots] package is used for plotting and the Statistics[stats] Package for some statistical analysis. LsqFit.jl[lsqfit] is used to fit the log-log plots to nice straight lines. PlutoUI.jl[plutoui] is used for some UI elements such as the ToC

7.8 μs

hidden code cell

7.5 ms

Define Structure and Functions

A Sandpile grid is nothing but an Integer Array and doesn't need any special definitions. We just need to define the functions that act on a 2 dimensional grid which can simulate the rules of a Sandpile model

7.1 μs

The Sandpile model

In the most abstract sense, a Sandpile is just an array of integers which evolve in a specific way. However, more intuitively, it can be thought of as a distributions of equally sized grains of sand on a discrete grid. Then, the array of integers represent the height or the slope of the pile in that location. Note that in the following report, we think of the values as the slope of the pile. However,

The use of Height

We use height to simply refer to the value of the cell, not the actual height of the pile. This poor choice of words is a common tactic to confuse readers so that they don't read the paper too carefully and find mistakes.

Method of evolution

The model evolves with the following algorithm -

$z_{i, j} (t + 1) = z_{i, j} (t) - h_{c} (z_{i, j} (t) > h_{c}) + count (n \to h_{c} > n, neighborhood)$

Basically, we define a neighborhood of $h_{c}$ cells. If the height of the sand in a cell is greater than $h_{c}$ , it is in a critical state, $h_{c}$ grains topple into the neighboring cells equally. Hence, we can simply subtract $h_{c}$ and count the number of critical neighbors to calculate the value of the cell in the next time step. Note that the sand is conserved in this form of evolution.

Relevant Quote

Waste not the smallest thing for grains of sand make mountains

- Eric Knight

15.2 μs

Our neighborhood and $h_{c}$

In this work, we use the VonNeumann Neighborhood in 2D and radius 1. Hence, the neighbors are $(- 1, 0), (+ 1, 0), (0, - 1), (0, + 1)$ and $h_{c}$ = 4

4.4 μs

              
xxxxxxxxxx
 
hc = 4

200 ns

iscritical (generic function with 1 method)

              
xxxxxxxxxx
 
@inline iscritical(i::Int, hc::Int) = i >= hc

99.8 μs

evolveat (generic function with 1 method)

              
            
xxxxxxxxxx
 
function evolveat(
        grid::Array{Int,2}, 
        hood::Array{CartesianIndex{2},1}, 
        index::CartesianIndex, 
        hc::Int,
        topple::Array{Int},
        affected_grid::BitArray{2},
        step::Int
    )
    res = grid[index]
    if res >= hc
        res -= 4
        @inbounds topple[step] += 1 # we'll talk about this later
        affected_grid[index] = true # and this
    end
    c = count(h -> iscritical(getindexbc(grid, h + index), hc), hood)
    res = res + c
    return res
end

              

95.6 μs

Boundary Conditions

We use a fixed boundary condition of 0. This is like the edge of a table, because all sand keeps falling and is lost forever.

Relevant Quote

Summer Vacation is slipping through our hands like grains of sand!

- Calvin from Calvin and Hobbes

6.4 μs

getindexbc (generic function with 2 methods)

              
            
xxxxxxxxxx
 
begin
    @inline function getindexbc(grid, i)
        if checkbounds(Bool, grid, i)
            @inbounds return grid[i]
        else
            return 0
        end
    end
    getindexbc(grid) = i -> getindexbc(grid)
end

              

114 μs

evolve! (generic function with 1 method)

              
            
xxxxxxxxxx
 
function evolve!(
        grid::Array{Int,2}, 
        simgrid::Array{Int,2},
        affected_grid::BitArray{2},
        hood::Array{CartesianIndex{2},1},
        hc::Int,
        topple::Array{Int,1},
        step::Int
    )
    for index in CartesianIndices(grid)
        @inbounds simgrid[index] = evolveat(grid, hood, index, hc, topple, affected_grid, step)
    end
    return simgrid, grid
end

              

63.3 μs

Sanity Check and Pretty Animations

Let's run a small simulation on a 10x10 grid to see if we've coding in everything correctly. We start with an empty Pile and add a grain in the center of the grid. We wait for the pile to relax, and we add another grain of sand. We do this until we add 100 grains of sand.

19.4 μs

42.0 s

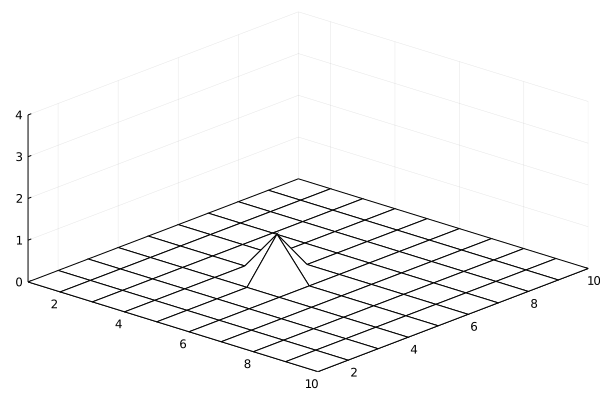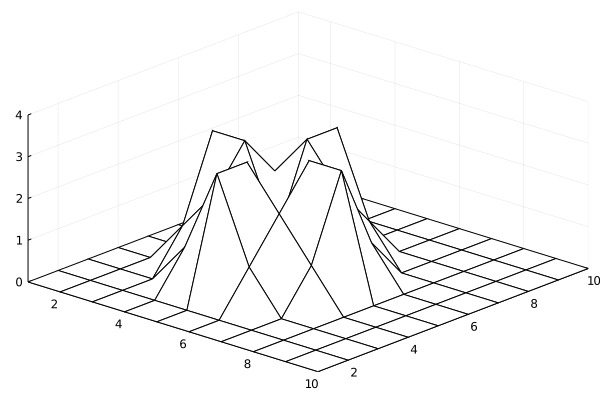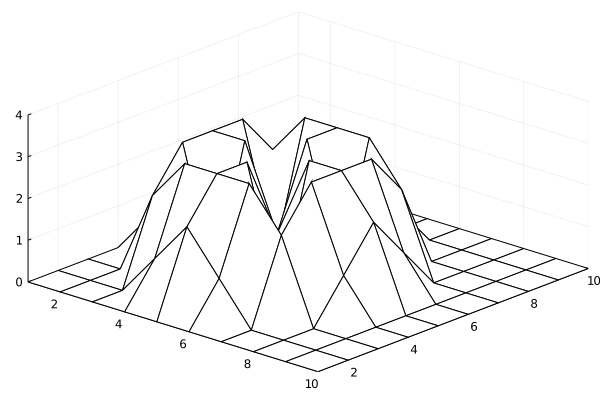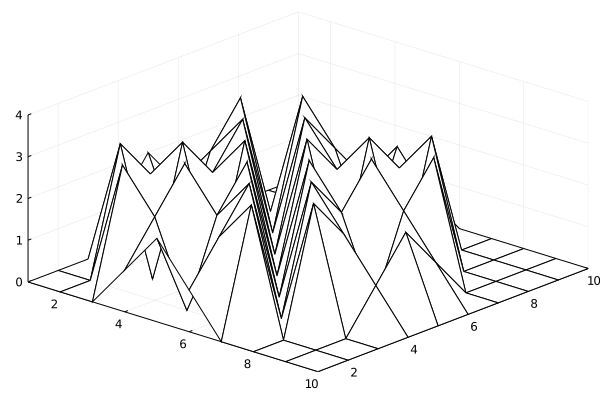
hidden code cell

14.1 μs

Observations

The pile builds up to a height of 4 and then topples, as expected
The pile falls off at the edge, as expected
Some topplings are quick where as some topplings set off another topple and so on. However, these chained topples are not as common as the single or double topples. We'll call an entire chain of topplings until a sand grain is added as a avalanche
This looks NOTHING like an actual sandpile. What were the authors thinking?

Regarding point 4, this is because we are keeping a track of the slope, not the height of the Sandpile. And yet we called it the height. I warned you, this is super confusing.

5.5 ms

Power law analysis

According to the paper mentioned before, there are certain properties which show a log-log frequency plot, which means that

$\log (F_{x}) = m \cdot \log (x) + c$

for certain properties of the model, where x is the value of the property and F(x) is the frequency of the value. These properties are -

Number of sites affected during an avalanche
Total number of topples induced during the avalanche
Relaxation time of the avalanche

Lets elucidate this further. Given a random condition, a single perturbation may lead to the pertubed cell to topple. This may, or may not, set off an avalanche which affects neighboring cells, has multiple topples, and takes a while to settle down. If we count these properties, and plot them on a log-log plot, it was shown that they form a straight line.

23.9 μs

Short note on Implementation

The properties are measured in the following fashion

- Toggle count - The $i^{t h}$ element of an array is updated everytime a topple is simulated in the $i^{t h}$ perturbation.
- Relaxation Time - The $i^{t h}$ element of an array is updated after every evolve cycle for the $i^{t h}$ perturbation.
- Number of sites affected - The $(i, j)$ element in a grid of falses is set to true when the $(i, j)$ cell topples in a perturbation (not evolve) cycle. At the end of the $k^{t h}$ perturbation, the total number of trues are counted and stored in the $k^{t h}$ element of an array.

3.9 μs

ready_next! (generic function with 1 method)

              
            
xxxxxxxxxx
 
function ready_next!(
        grid::Array{Int,2}, 
        affected_grid::BitArray{2},
        hc::Int,
        affect_count::Array{Int, 1},
        relax_time::Array{Int, 1},
        step::Int, max_steps::Int
    )
    if count(iscritical.(grid, hc)) == 0
        affect_count[step] = count(affected_grid)
        affected_grid[:] .= false
        if step == max_steps
            return false, step
        else
            # perturb
            xrand, yrand = rand.(Base.OneTo.(size(grid)))
            grid[xrand, yrand] += 1
            step += 1
        end
    else
        relax_time[step] += 1
    end
    return true, step
end

              

255 μs

simulate (generic function with 1 method)

              
            
xxxxxxxxxx
 
function simulate(grid::Array{Int}, hc::Int, max_steps::Int)
    hood = CartesianIndex.([(-1, 0), (1, 0), (0, -1), (0, 1)])
    topple_count = fill(0, max_steps)
    relax_time = fill(0, max_steps)
    affect_count = fill(0, max_steps)
    step = 1
    st = true
    simgrid = similar(grid)
    affected_grid = falses(size(grid))
    while st
        st, step = ready_next!(grid, affected_grid, hc, affect_count, relax_time, step, max_steps)
        grid, simgrid = evolve!(grid, simgrid, affected_grid, hood, hc, topple_count, step)
    end
    return topple_count, relax_time, affect_count
end

              

261 μs

Method of analysis

Once we've simulated and collect the data, the analysis is done in the following way-

Create a frequency table of val => freq(val) for each of the properties.
Take a log for both values and frequencies.
Fit the data to $freq = m \cdot val + c$
Smooth the data and plot it against the fit

Things to keep in mind while fitting

The data does not follow a linear curve completely. The linearity is lost for reasons listed below. Hence, we should fit the data to only the first, linear part of the data, which usually is around 60%

18.3 μs

freqtable (generic function with 1 method)

163 μs

getlogdata (generic function with 1 method)

58.2 μs

smooth (generic function with 1 method)

153 μs

loglogfit (generic function with 1 method)

72.2 μs

stringifyfit (generic function with 1 method)

47.3 μs

makeresults (generic function with 1 method)

135 μs

              
xxxxxxxxxx
 
data_50_1_5 = simulate(rand(1:hc - 1, 50, 50), 4, 100000);

139 s

Grid size = 50, Samples = 1e5

25.6 ms

              
xxxxxxxxxx
 
data_50_1_4 = simulate(rand(1:hc - 1, 50, 50), 4, 10000);

11.1 s

Grid size = 50, Samples = 1e4

16.7 ms

              
xxxxxxxxxx
 
data_50_5_4 = simulate(rand(1:hc - 1, 50, 50), 4, 50000);

69.7 s

Grid size = 50, Samples = 5e4

10.9 ms

              
xxxxxxxxxx
 
data_20_5_4 = simulate(rand(1:hc - 1, 20, 20), 4, 50000);

4.5 s

Grid size = 20, Samples = 5e4

11.4 ms

              
xxxxxxxxxx
 
data_80_5_4 = simulate(rand(1:hc - 1, 80, 80), 4, 50000);

265 s

Grid size = 80, Samples = 5e4

17.5 ms

mktable (generic function with 1 method)

68.9 μs

Result Summary

7.3 μs

Topple Count

Sample Size	20x20	50x50	80x80
1e4	No Data	-1.019±-2.785%	No Data
5e4	-1.106±-1.382%	-1.109±-1.361%	-1.064±-1.299%
1e5	No Data	-1.139±-1.078%	No Data

92.1 ms

Relaxation time

Sample Size	20x20	50x50	80x80
1e4	No Data	-1.008±-3.447%	No Data
5e4	-0.9078±-3.113%	-1.004±-1.806%	-1.066±-1.414%
1e5	No Data	-1.036±-1.491%	No Data

88.9 ms

Affected grids

Sample Size	20x20	50x50	80x80
1e4	No Data	-1.032±-2.849%	No Data
5e4	-1.051±-1.317%	-1.09±-1.419%	-1.073±-1.359%
1e5	No Data	-1.098±-1.063%	No Data

61.5 ms

Observations

All the values of slope lie within the range $[- 1.1, - 0.95]$
As the sampling size increases, the error reduces
As the grid size increases, the error reduces
The linear domain
- increases with sample size until a point, after which it doesn't increase further
- increases with grid size until a point, after which it doesn't increase further

20.4 μs

References

soc

Self-organized criticality. Bak, Per and Tang, Chao and Wiesenfeld, Kurt. (Jul, 1988) Phys. Rev. A, 38: 364–374. doi: 10.1103/PhysRevA.38.364

julia

Julia: A Fresh Approach to Numerical Computing. Jeff Bezanson, Alan Edelman, Stefan Karpinski, Viral B. Shah. (2017) SIAM Review, 59: 65–98. doi: 10.1137/141000671

plots

Plots - powerful convenience for visualization in Julia. Thomas Breloff. docs.juliaplots.org

pluto

Pluto - Reactive Notebooks for Julia. Fons van der Plas and Mikołaj Bochenski. https://github.com/fonsp/Pluto.jl

plutoui

PlutoUI. Fons van der Plas. https://github.com/fonsp/PlutoUI.jl

stats

Statistics - Julia stdlib for Statistics. https://docs.julialang.org/en/v1/stdlib/Statistics/

10.4 μs