IDC402 Non Linear Dynamics

Fractals

Countable and Uncountable sets

Any set that is bijective with $\mathbb{N}$ is called countable.

Consider $\mathbb{E} = {\text{even numbers}}$ which can be written as

\[\mathbb{E} = {2n \vert n\in \mathbb{N}}\]

But $\mathbb{R}$ is uncountable can be shown by contradiction. Let $[r_i]$ be the binary expansion of every $r$ in $\mathbb{R}$. Assume that $\mathbb{R}$ is countable, therefore all $r$ can be indexed by some variable $j$.

Now consider $x$ which has a binary expansion where $x_j = ~r_{j}^j$. This $x$ is different from every $r^j$ at the $j$th position, which is a contradiction.

Fractal Sets - Cantor set

Consider a line from $l_0 = [0, 1]$. Generate $l_1$ by removing $[1/3, 2/3]$. Generate $l_2$ by removing the middle third of each segment. Then, the Cantor set is defined as all the points in $l_\infty$

What is the measure of this Cantor set?

Any $l_i$ must be smaller than $l_j$ for all $j<i$. Hence, $l_\infty$ must be smaller than all $l_i$.

Now $l_i$ has a length of $(2/3)^n$. Hence, taking $\lim_{n\to\infty}$ gives a length for $l_\infty = 0$

How many points in the set?

Consider the ternery expansion of any $r$ in $[0, 1]$. It is of the form $r = \sum r_i (1/3)^i$ where $r\in {0, 1, 2}$. Geometrically, $r$ lies in the $r_ith$ third in the $r_{i-1}th$ segment. Hence, the Cantor set is the set of all points which don’t exist in the second third in any segment. This implies that they don’t have a $1$ in their ternary expansion. Now to show that the Set is uncountable, we again assume that it is countable, and generate an $x$ such that $x_i = 2 - r^j_j$ which will not be a part of the set, exactly like in [#Countable and Uncountable sets|Real numbers]

Hence, the Cantor set has uncountably many points but still has a measure of 0

Dimensions of Fractals

Similarity dimension

This is given by looking at how many more scaled self similar parts we need to make every part of the fractals.

If $m$ is the number of scaled, and r is the scaling parameter, then the similarity dimension is given by

\[d_s = \frac{\ln m}{\ln n}\]

For example, a box can be covered by $r^3$ boxes scaled by r boxes.

For the Koch curve, we need 4 lines of size 1/3 to cover each step of the Koch sequence. Hence, the dimension is $\ln4/\ln3)$

For the Cantor set, we need 2 lines of size 1/3 to cover each $l_n$. Hence, $d_{s} = \ln2/\ln3$

Statistical Fractals

This are fractals where self similarity is only statitstical and not exact.

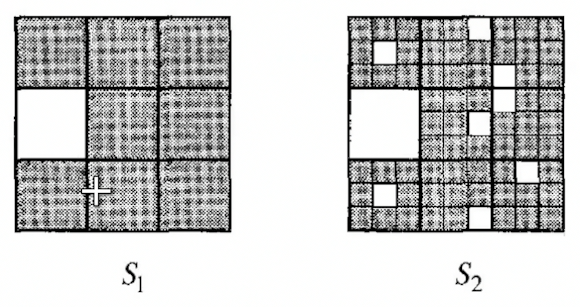
In such cases, we cannot define the Similarity dimension, and we need to introduce other

Box Dimension

It is the number of boxes of size $\epsilon$ needed to cover the set as $\epsilon$ tends to 0.

\[d_b = \lim_{\epsilon\to 0} \frac{\ln N(\epsilon)}{\ln\frac{1}{\epsilon}}\]

For the Koch curve, we take $\epsilon = 1/3^n$. We need $4^n$ such segments. Hence, taking $\lim_{n\to\infty}$, we get $d_b = \frac{\ln(4^n)}{\ln(\frac{1}{1/3^n})}=\frac{\ln 4}{\ln 3}$

For the Cantor set, we take $\epsilon = 1/3^n$. We need $2^n$ such segments. Hence, taking $\lim_{n\to\infty}$, we get $d_b = \frac{\ln(2^n)}{\ln(\frac{1}{1/3^n})}=\frac{\ln 2}{\ln 3}$

For the 8/9 statitstical Fractal, the box dimension can be found by $\epsilon = 1/3^n$, and $N = 8^n$. Hence we get $d_b = \frac{\ln8}{\ln3}$

Point Dimension

For dynamical maps, we cannot define such a dimension.

One way to define the dimension is to take the average density of an orbit at each point. Hence, the box dimension weighs each box equally, whereas the point/correlation dimension weighs each point by density.

$d_\text{corr} \le d_b$

\[d_{correlation} = \frac{\ln C(\epsilon)}{\ln \epsilon}\]

This $C(\epsilon)-\epsilon$ curve generally saturates at very small $\epsilon$ and very large $\epsilon$. For large $\epsilon$, the ball is so big that it engulfs the entire orbit. For small $\epsilon$, the sample size is not large enough, which leads to no points being recorded.