IDC402 Non Linear Dynamics

Monday, February 08, 2022

Quantitative Classification of Chaos

We define the Lyaponov exponent $\lambda$ as

\[|\delta_n| = |\delta_0|e^{\lambda n}\]

Noting that

\[|\delta_n| = F^n(x+\delta) -F^n(\delta)\]

Hence,

\[\lambda = \frac{1}{n}\ln\frac{F^n(x+\delta x) -F^n(x)}{\delta_0} = \frac{1}{n}ln |(F^n)'(x)|\]

And using Chain rule,

\[|(F^n)'| = \prod_{i=1}^n |F'(x_i)|\]

Here, we have shifted the derivative of the nth iterate to the product of derivatives over the trajectory.

Finally,

\[\lambda = \lim_{n\to \infty} \frac{1}{n}\sum_{i=1}^n \ln|F'(x_i)|\]

Clearly,

$\lambda$ depends on $x_0$, but for a particular basin of attraction, it is same. This is because all points in this basin finally reach the same orbit, and in large n limit, the transince period does not matter.

Values and Classification

Stability

$\lambda < 0$ is stable points and $\lambda > 0$ is Chaotic.

$\lambda = \ln 0 = -\infty$ is super stable.

Lyaponov for some maps

For the tent map, $\lambda = \ln 2$

For logistic map however, the $\lambda$ depends on $x$

\[\lambda = \frac{1}{n}\prod_i^n \ln(|r-2rx|)\]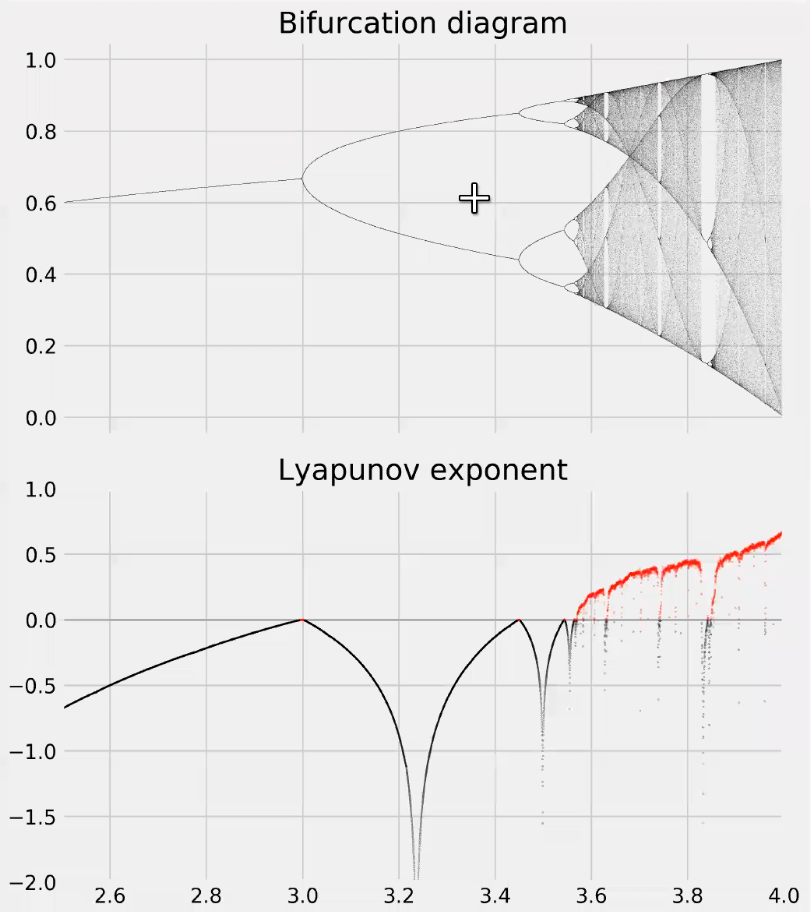

Renormalization

1. Let $f(x, r)$ be an unimodal which goes through period doubling to chaos
2. $x_m$ is the maximum of $f(x, r)$$
3. $r_n$ is where $2^n$ cycle bifurcation
4. $R_n$ is super stable cycle of period $2^n$

Example

For example,

$f(x, r) = r - x^2$

$R_0,\ R_1$

$R_0$ must also be a period 1 cycle.

$x^* = R_0 - x^{*2}$

$f’(x^*, R_0) = 0$

Hence, $x^* = 0$, and hence,

\[R_0 = 0\]

$R_1$ must be cycle 2, and super stable at two points.

Let $x_1$ and $x_2$ be the cycle,

$F’(x_1)*F’(x_2) = 0 \implies 4x_1x_2 = 0$, and hence, wlog $x_1 = 0$

Now, from the period 2 condition,

$F^2(0, r) = r - r^2 = 0\implies r = 0$ or $r=1$. But $R_0=0$, and hence, $R_1=1$

All period 2 cycles are self similar, and we can compare $f(x, R_0)$ and $f^2(x, R_1)$

At the maxima, unimodal maps have a order 2 approximation. Hence we can

1. Translate $f$ to $x_m$ st $x’ = 0$ is a maxima
2. Subtract $x_m$ from $f$, since $f(x_n, r)=x_{n+1}$
3. Then scale $x’_n$ and $y’_n$ by dividing $x_n \to x_n/\alpha$ and $f^2\to \alpha f^2$

Hence

\[f(x, R_0) = \alpha f^2(x/\alpha, R_1)\]

We can repeat this and more generally,

\[f(x, R_0) = \alpha^n f^{2n}(x/\alpha^n, R_n)\]

Figenbaum universality

Taking the limit of $n\to \infty$

\[\lim_{n\to\infty} \alpha^n f^{2n}(x/\alpha^n, R_n) = g_0(x)\]

Is this function $g_0$ independant of $f$? Turns out this is true because we are blowing up smaller and smaller sections of the function ($x\to x/\alpha^n$) and ignoring the rest.

However, $g_0$ does depend on the order of $f$

$g_i$

Instead of starting from $f(x, R_0)$, we can start with other $i$

\[\alpha^nf^{2n}(x/\alpha^n, R_{i+n})\]

Taking $i\to \infty$, this reduces to

\[f(x, R_\infty) = \alpha^n f^{2n}(x/\alpha^n, R_\infty) = g(x)\]

Taking $n = 1$ we get the self referential equation,

\[g(x) = \alpha g^2(x/\alpha)\]

By setting $g’(0) = 0$ ($x_m=0$), and $g(0) = 1$ (we can scale accordingly).

Hence, $g(0) = \alpha g^2(0) \implies 1 = \alpha g(1) \implies$

\[\alpha = 1/g(1)\]

Finding $g$ however is difficult, but we can solve this using power laws.

\[g(x) = 1 + c_2x^2 + c_4x^4+\dots\]

By putting this back into the self referential equation and matching terms, we get $g$