IDC402 Non Linear Dynamics
Tuesday, January 25, 2022
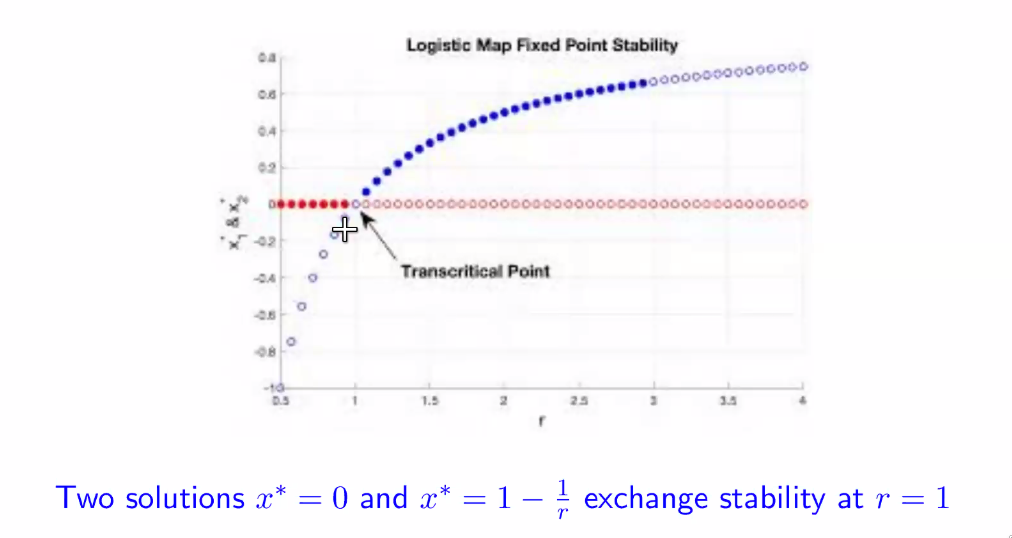
Transcritical Bifurcation
- Two solutions exchange stability
At $r = 3$, Period 1 cycle becomes unstable, and at the same time Period 2 cycle comes into being.
$r_i$ is the value of the parameter $r$ when Period $2^i$ crosses to $2^{i+1}$
$r_0=3$
$r_1 = 3.449$
$r_2 = 3.45$
Infinite cascade of period doublings keeps narrowing, and $r_{\infty} \approx 3.57$.
Solving for the Period 2 cycle
We need to solve the Degree 4 equation of $F^2(x) = x$. However, we know 2 of the solutions which can be factored out and the quadratic equation can always be solved.
On solving,
\[x^*_{2_\pm} = \frac{r \pm \sqrt{(r-3)(r+1)}}{2r}\]These are real only for $r>3$. So 2 cycle exists for all $r>3$. 2 cycle does not exist for $r<3$.
Stability of the 2 cycle
Trivially,
- at $x^*=0$, $\lambda = r^2$. Hence, it is always unstable.
- Similarly, we can evaluate for $x^* = 1- 1/r$
For the 2 cycle, $\lambda_2 = F^\prime(x_1)F^\prime(x_2)$. To analyse the stability, reduce the question of stability of a fixed point. Both are solutions of $F^2 = I$. We can use the above solutions to get $\lambda_2 = 4+2r-r^2$. Hence, $3<r<1+\sqrt{6}$ is where the 2 cycle is stable.