IDC402 Non Linear Dynamics

2022-01-07

Approximately close initial conditions do not give rise to approximately close final conditions.

There are systems of $N = 3$ which show chaos. We need atleast $N=3$.

Iterated maps.

Consider a non invertable map $f$. An Iterated map orbit is defined as $I_n(x_0) = f^n(x_0)$.

This is a peicewise linear map

\[f(x) = 1 - 2|x-\frac{1}{2}|\]

Thats is,

\[\begin{cases} 2x & x < 1/2\\ 2(1-x) & x>1/2 \end{cases}\]

For x < 0 or x > 1, the orbit is uncontained.

However, for 0 < x < 1, the orbit is bounded.

Stretching - Half the interval is stretched to the entire interval.

Folding - the Folding makes the orbit bounded.

Tent with x_0=

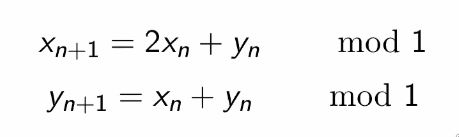
Cat Map application on a Map

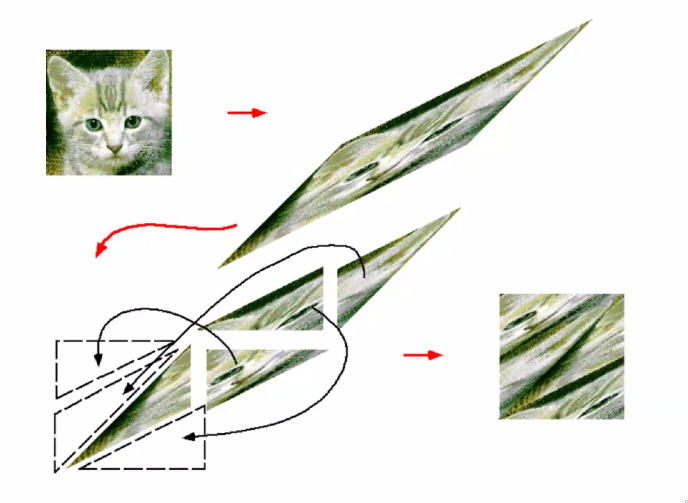
The map first stretches in the x direction, but it is cut and folded, put back into the box.

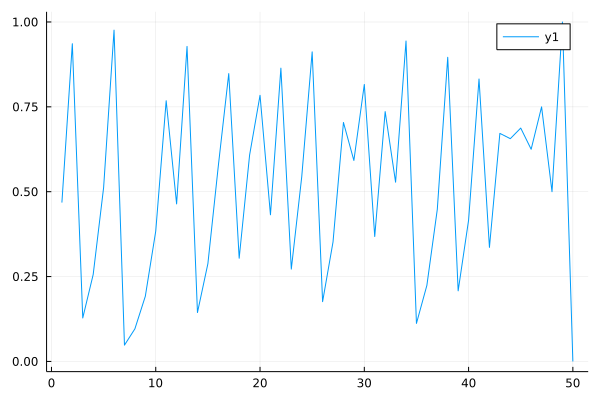
If $x_n$ = 0, 1/2, 1, then $x_{n+2} = 0$

If $x_n$ = 1/4, 3/4, then $x_{n+2} = 1$

Linear in between.

Hence, m iteration gives m tents.

If $\epsilon_0 = 1/2^m$ then $x_m$ can be anywhere between [0, 1]