HSS646 Principles of Economics

Thursday, January 27, 2022

Budget Line

$P_{1} x_{1} + P_{2} x_{2} \leq m$ $P_{1} x_{1} + P_{2} x_{2} = m$ where, $P_{i}$ is price of $i$ with quantity $x_{i}$ and $m$ is income.

Since income and $P_{i}$ is constant,

$P_{1} d x_{1} + P_{2} d x_{2} = 0$ Hence, $\frac{d x_{1}}{d x_{2}} = - \frac{p_{2}}{p_{1}}$

This is the slope of the budget line.

Variation in budget lines

Therefore, the budget curve changes as income or price levels change.

Income changes

This shifts the line to the right (left) as income increases(decreases).

Slope remains same

Price Changes

When price changes, the intercept moves towards(away from) origin as price increases(decreases).

\text{Slope}

c h a n g e s l i n e a r l y i n

P_1

a n d i n v e r s e l y

P_2$, but remains negative.

Effect of Tax, Subsidy and Rationing

What does imposition of tax mean to a customer?

Price of good increases. Hence, budget line changes, as above

Subsidy on quantity

Price of good decreases. Hence, budget line changes, as above

Rationing

Along with the above budget line equality, we have additional constraint $x_{i} \leq x_{i}^{*}$

Indifference curve

They cannot intersect

Perfect substitute and Compliments

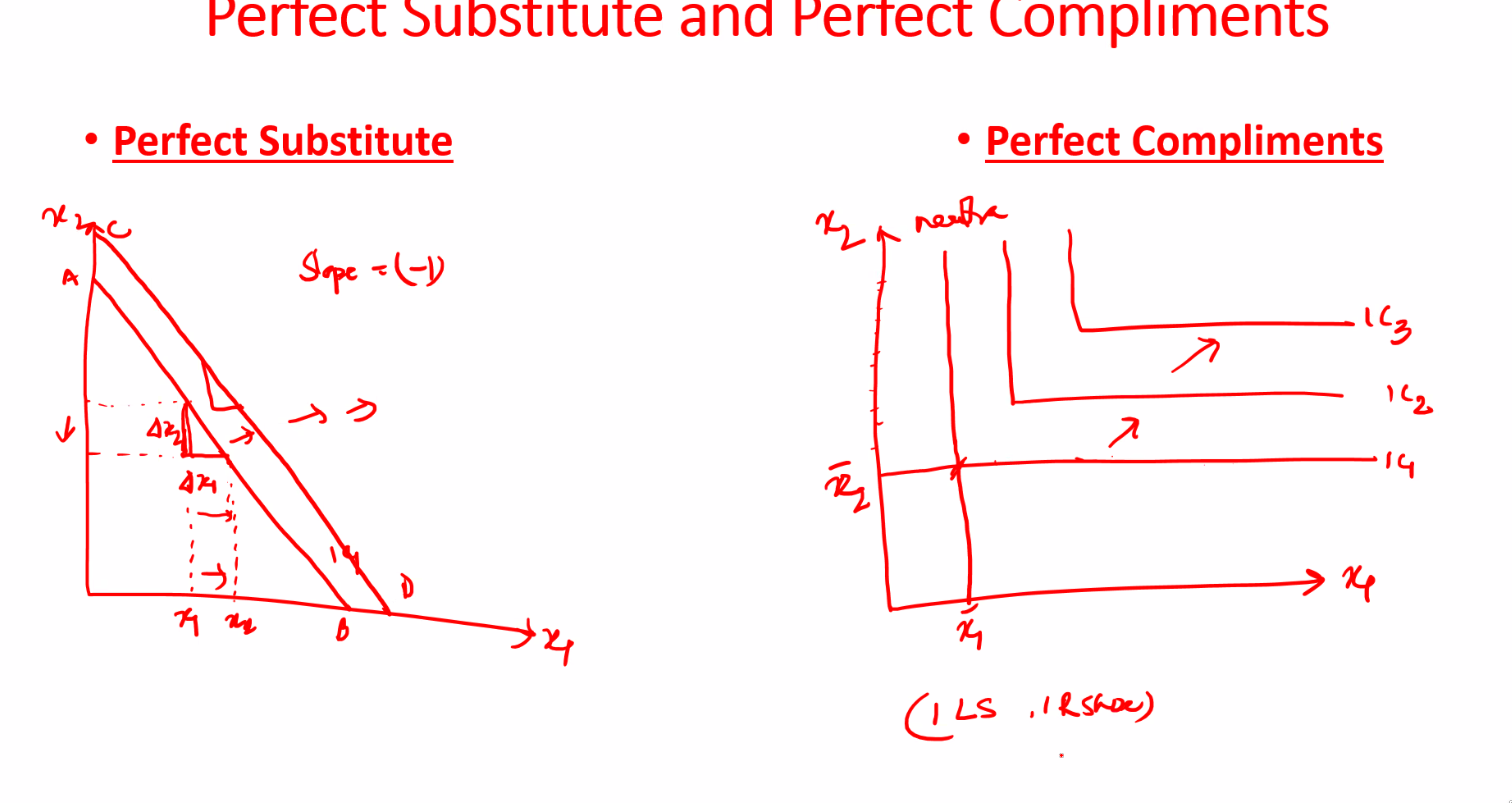
Substitutes - slope is 1 of budget curve
Perfect Compliments - L shaped budget curve

Consumer Choice and Consumer Equilibrium

$u = f (x_{1}, x_{2}) = k$ $d u = \frac{\partial u}{\partial x_{1}} d x_{1} + \frac{\partial u}{\partial x_{2}} d x_{2}$ $\frac{\frac{d u}{d x_{1}}}{\frac{d u}{d x_{2}}} = - \frac{d x_{2}}{d x_{1}}$ $\frac{M u_{1}}{M u_{2}} = - \frac{d x_{2}}{d x_{1}}$

Equal marginal Principle

Aim is to maximize utility subject to budget curve.

Hence, we define Composite utility function using the lagrange multiplier definition.

P ({x_{i}}) = U ({x_{i}}) - λ (\sum_{i} p_{i} x_{i} - M)

\frac{\partial F}{x_{i}} = \frac{\partial u}{\partial x_{i}} - λ p_{i} = 0

Hence,

\frac{\partial u}{\partial x_{i}} = λ p_{i}

\frac{m u_{i}}{p_{i}} = λ = \frac{m u_{i}}{p_{i}}

Hence, $\frac{M u_{1}}{M u_{2}} = \frac{p_{1}}{p_{2}}$

$M R S_{x_{1}, x_{2}} = \frac{M u_{1}}{M u_{2}}, \frac{p_{1}}{p_{2}}$

$M R S$ is the slope of the indifference curve

$\frac{p_{1}}{p_{2}}$ is the slope of budget curve.

Hence, the equilibrium point is when slope of indifference curve is equal to slope of budget line. Therefore, E is where the budget line is tangential to the indifference curve.